What Is A Strip Diagrams In Math?
A strip diagram, sometimes known as a bar model, length model or fraction strip, is a kind of visual model used when teaching math in order to demonstrate numerical relationships and help students solve various numbers and problems a little more easily.
A strip diagram is essentially a rectangular bar or box that can be divided up in different ways to represent known and unknown quantities.
The overall idea is that with a drawing or picture students can better visualize a problem and then decide what operation they should use to get the answer.
How Are They Used In Math Lessons?
Strip diagrams are actually pretty flexible visual tools that can be used when learning different topics and when confronted by different types of word problems.
Typically, strip diagrams are used as a tool to help students visualize problems and what operations they’re being asked to do (addition, subtraction, multiplication and division), something that can be particularly helpful with word problems.
The overarching principle is that, by drawing out a model, students learn to pick out the different variables given in a word problem, what they need to find and can then figure out what operation and methods they need to use to solve the problem in question.
Different types of strip diagram strategies
In general, there are a few different ways that parents and teachers use strip diagrams to solve different math problems.
Part-Part Whole/Equal parts of a whole
Generally speaking, the first strip diagram most students will learn is the part-part whole model.
In essence, a large rectangle is placed at the top, representing a whole amount.
Below it, a same-sized rectangle is divided up into two or more pieces, representing the different parts that can make up that whole.
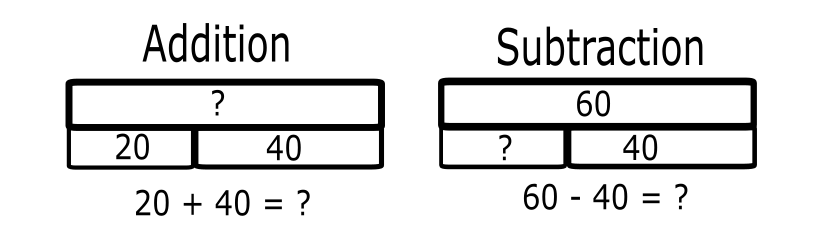
Depending on the problem, these can be uneven in size (representing two different numbers – such as in an addition or subtraction) or equal in size.
A bar might even be broken down into several, separate parts, as might be found in multiplication and division.
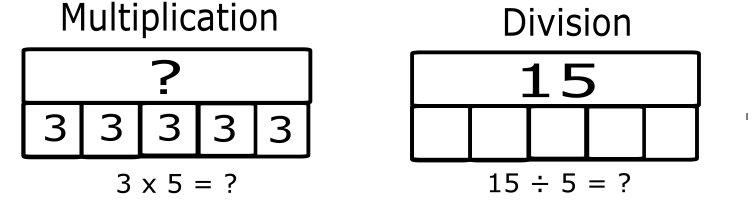
Students are given some information but quickly realize they are going to find and fill in the missing pieces.
Comparison strip diagram
Compariston strip diagrams are, much as the name would imply, an intuitive and visual way of approaching problems where there is a difference in amounts and when there is a known/unknown component.
They can be ideal, for example, when approaching problems that ask the student things like:
- How much more than
- How many more
- How many fewer
- Larger than
- Smaller than
- And so on
Much like Part-Part Whole models, comparison strip diagrams have two bars arranged one on top of the other so that students can immediately grasp the difference in length between the two, with brackets pointing out relevant numbers and totals.
The idea here is that these very visual bars can be an easy starting point for understanding differences in amounts.

More than that, however, we find that they can make understanding and breaking down comparison word problems a little easier for students, especially given the wide variation in vocabulary and terms that these problems can use (taller than, wider than, bigger than, as many as, as few as, fewer than, greater than, more expensive than, etc.).
Using strip diagrams for more complex problems
One common misconception is that strip diagrams are only used for basic operations such as addition, subtraction, multiplication and division.
The reality is they are quite flexible and can be used well into more advanced math and for more complex and tricky word problems that often throw students.
For example, strip diagrams can be used to illustrate and work out ratio problems, such as below.

How To Set up A Strip Diagram Effectively
It’s important to keep in mind that strip diagrams are a tool and that a good homeschooling parent can’t be too rigid when it comes to its precise use and application.
It goes without saying that one needs to keep a student’s unique personality, understanding, abilities and skills in mind when doing any kind of problem solving.
That said, there are some steps that most programs will involve when teaching students to use a strip diagram. These tend to be:
- Read the question carefully and to completion.
- Highlight or circle any important information provided in the question, paying special attention to numbers and important words or phrases (more, together, as many).

- Find the variables “who” and “what” – in particular:
- Who is the problem about/what is the problem about
- What is known
- What information is missing
- Rereading the key phrase of the question (and paying special attention to any particular phrases – how many, what is the total, who/what is bigger, how much, etc), decide what operation needs to be used to solve the problem.
- Draw and label the bars using the information collected
- Review the problem to make sure the bars make sense given the information presented
- Complete the calculation using the operation in order to work out the answer

Why Some Curricula Use Strip Diagrams
A systematic approach to confusing word problems
Younger students often struggle with word problems for a variety of reasons.
For one thing, word problems (unlike computational exercises) involve much more than math.
Rather than being presented with a straight forward math problem, students are suddenly faced with a paragraph of words and numbers.
From this jumble of words, they have to keep track of a lot of different information, figure out what’s important, determine what the question actually is (since it’s usually cloaked in specific math vocabulary) and, finally, they have to figure out what to do.
Strip diagrams can help by providing students with a ready and systematic method of approaching these problems.
In order to build a strip diagram, students need to parse out the important information, collecting information on:
- What the problem is about
- What information is given to me
- What information is missing
As a student gets more practice in building strip diagrams, they can become more adept at highlighting key information, ignoring irrelevant information, and identifying key math terms as hints for what the operation is supposed to be about.
In addition, as they get more experience at drawing out these diagrams, they can get better at organizing and presenting that information in a meaningful and more organized way, something that’s helpful for students who have a hard time showing their work or communicating their thoughts succinctly or mathematically.
Visual approach to help younger students with abstract concepts
Another challenge word problems present is that they often challenge students to reason or think through problems abstractly.
Typically, below the age of 12 or so, students are far better at seeing the world in concrete terms than they are at understanding abstractions.
They think logically, sure, and they can understand symbols for the most part, but the way in which they tend to understand things best is by being able to directly observe it.
A word problem involving two trains speeding along the track between two cities, or age differences between several kids, or different sizes of different items, or different prices can all be very hard for kids to get their heads around.
Learning to build a strip diagram can help younger students by letting them see and work with a visual (and concrete) representation of the question’s information rather than just relying on the written word.
A gentler introduction to algebraic thinking
Yet, it’s important to note that despite being visual, strip diagrams still remain somewhat symbolic and standardized, abstracted to a degree from the various topics and characters that pop up in a word problem.
Students are working with rectangles, after all, and aren’t being asked to literally draw out every problem.
As a result, they can still act to help kids get used to algebraic thinking, that is the ability to represent, generalize or reason through a problem using abstract math symbols and relationships.
There is strong evidence for their usefulness
Being something of a different way to tackle word problems than many educators (and parents) are used to, some have questioned whether using strip diagrams in approaching math problems has any real effect on success.
In recent years, studies have been run measuring how well strip diagrams can help students understand and solve math operations and word problems.
The findings from these have been quite positive. Studies have found, for example, using strip diagrams as a tool can be effective in helping elementary students answer word problems correctly, and there is some evidence that it can be an effective tool for remediation.
Pros and Cons of Using Strip Diagrams in your Homeschool Learning
It is important to remember that strip diagrams are just one of many tools that parents and students can use to solve word problems.
It is also important to note that, as a tool, strip diagrams can have their pros and cons and integrating their use into teaching isn’t always the best fit for every student.
Advantages of Strip Diagrams
Easy to learn for both parents and students
Learning to use strip diagrams and weaving them into a problems solving approach isn’t really all that hard once you get the hang of it.
By and large, strip diagrams are really just a particular way of sketching out the key details of a question in a few different ways and can be pretty intuitive for both parents and students to learn and use.
Easy to understand, visual representation of word problem information
As mentioned previously, creating a strip diagram provides students with a pictorial representation that they can use to better understand what they’re being asked to do.
Seeing the size difference between two or more squares can be a lot easier to deal with for students than a paragraph involving trains, planes, clothing, chocolates, people, heights, sizes and more.
Encourages students to break apart and analyze word problems systematically
In order to set up a strip diagram properly, students have to learn to read a sentence, identify key elements, identify what is missing and understand certain important key phrases.
As a result, practicing strip diagrams can help students learn to approach word problems (and lay out their results) in a more organized and logical manner.
Easy to integrate with manipulatives and hands-on learning objects
Strip diagrams lend themselves quite easily and naturally to hands-on math learning approaches.
Strips can be constructed using blocks, pennies, sticks or whatever else might be handy, turning learning into a multisensory activity that can better suit tactile learners.
Disadvantages
Not every student needs to use strip diagrams (or wants it)
Although a useful tool, strip diagrams aren’t a tool that every student needs or prefers to use.
Some students “get” word problems very easily, being able to almost intuitively pick out key information and have no problem thinking about and representing them using equations and symbols.
Other students are more procedural in nature and don’t much care for the use of visuals and other models. Such students might prefer a more straightforward, by the numbers approach to solving word problems (i.e. memorizing a series of steps to follow) or may simply respond well to more practice and drill.
In either case, such students may find being forced to use strip diagrams frustrating.
In the case of more gifted math students they may even see the process as superfluous and something of a burden on them.
It can slow things down when solving problems
Strip diagrams do involve identifying and collecting information from a word problem, organizing it and drawing a model that makes some kind of sense in terms of scale.
Consequently, setting up and working with strip diagrams can take time, especially when students are still getting the hang of the process, which in turn can increase the length of a math lesson or practice session.
Not applicable to all word problems in math
While they tend to work well for most word problems involving operations and even algebra, creating strip diagrams doesn’t always make sense (or even really work) with all types of math problems.
Statistics and geometry, for example, can have interesting and challenging word problems associated with them but don’t necessarily lend themselves as subjects to strip diagrams and require their own models and algorithms to follow.
What Curricula Use Strip Diagrams And Other Easier Math Tools?
Strip diagrams, in particular, are most notably (although not exclusively) a characteristic of programs based on the Singapore approach to math and these programs tend to do a pretty good job at guiding parents and students through their use in a step-by-step manner.
The Singapore approach to math (so-called as it was originally developed as the main math curriculum for elementary school students in Singapore) is a conceptual math method that focuses on teaching students the why behind math and why it works the way it does, as well as to think critically and to solve math problems without relying excessively on memorization and drill.
In doing so, and by teaching for mastery, these programs tend to give students a deeper understanding of number relationships, strong math fluency and problem solving skills compared to more traditional programs.
The Singapore method or approach believes very strongly in what they call the Concrete-Pictorial-Abstract stages of learning, i.e. bringing a student gently from the concrete stage of understanding through a visual modeling stage and finally to a point where the student is comfortable using abstract symbols and equations.
Alongside number bonds, strip diagrams (which are more commonly referred to as bar models in these programs), tend to fit comfortably in the visual/pictorial stage of learning.
If this type of math program interests you or you have a student who you think would benefit from approaching math problems more visually, such as with strip diagrams, then we highly recommend the following programs.
Singapore Math
One of the most famous and widely used examples in the homeschool community of the Singapore approach, Singapore Math offers a thorough and rigorous math curriculum for students in K-8 that emphasizes hands-on learning and visual representation of math problems.
Offering a couple different editions (Primary Mathematics and Dimensions), Singapore Math’s visually-rich books encourage a deeper, critical thinking approach to math that has produced very strong and capable math students over the years
Read our in-depth review of Singapore Math
Read our in-depth review of their latest curriculum Primary Mathematics 2022 Edition
Math in Focus
Released in 2009, produced by Marshall Cavendish and published by Houghton Mifflin Harcourt, Math in Focus is also based on the Singapore approach, teaches math similarly and also offers a rigorous and thorough math curriculum.
Singapore Math and Math in Focus are similar and the difference largely lies in the fact that Math in Focus is designed a bit more as a traditional school book, touches on a little more content and tends to have a little more built-in differentiation help.
Read our review of Math in Focus
Bottom Line:
A popular math model often associated with the Singapore approach, a strip diagram can be an excellent tool to help students more effectively deal with word problems.
While not always for every student, stripe diagrams can help students systematically analayze a complex word problem, better visualize what they are being asked to do and communicate their results in an organized manner.
And, for some students at least, that can make all the difference.

About the Author
David Belenky is a freelance writer, former science and math tutor and a tech enthusiast. When he’s not writing about educational tech, he likes to chill out with his family and dog at home.
